膜结构的载荷分析
2013-06-24 by:广州有限元分析、培训中心-1CAE.COM 来源:仿真在线
关键字: ANSYS 膜结构 膜材料 载荷
对膜特别是张拉膜结构而言,载荷静力分析考虑的主要是静风载、雪载、膜材自重等等。非线性有限单元法不仅适用于初始形态分析,而且也适用于静力分析。膜结构在载荷作用下变形是较大的,因此,常用的小变形理论不适用于膜结构分析,分析中必须考虑非线性因素,有时是强非线性,包括材料非线性和几何非线性。但是在实际结构中,膜中应力变化范围不是很宽,应力低于材料的弹性极限应力,所以可以认为应力应变关系仍处于线性阶段,材料的非线性可以不加以考虑。这样做可以将实际问题得到很大的简化,并且计算结果与实际结果相差也不大。
膜结构的有限元分析与其他结构的有限元分析的区别如下:
1)由于膜材的高度非线性,采用稠密网格划分的低精度单元比采用稀疏网格划分的高阶单元具有更高的精度;
2)结构具有特定的非线性方程组迭代收敛条件和判断准则,并要对松弛和褶皱区进行判断和处理。单元松弛和褶皱可通过主应力值进行判断:设单元的主应力 在载荷分析中,平衡方程不再是线性的了。在载荷分析中若发现结构变形过大,出现受拉单元或单元应力超过极限,则说明结构的刚度和强度不够,应该采用增加诸如初始预应力的措施来增加结构刚度,或采用强度更大或更厚的膜材,然后从初始形态确定开始,对结构重新进行修正。
对于膜结构的分离模型和整体模型,已有资料表明:
1)考虑整体模型时,由于下部钢结构变形会造成膜结构张力刚度下降,因此对找形会产生很大的影响。分离模型对支撑钢结构的设计偏重于安全,但是高估了膜的初始应力水平,膜实际张拉成型后很有可能难以达到设计时的应力状态。
2)两种计算模型的力学响应变化规律相似,但是数值差异较大,特别是整体刚度较低的张拉膜结构会产生不可忽略的差别。
3)由于整体模型在相同的初张力作用下,结构刚度下降,其自振频率整体呈下降趋势,但是变化不是太大。
下面对膜结构载荷理论做一个简要的说明。
薄膜结构力学分析采用的是与一般刚性结构力学分析相同的步骤进行的。所不同是必须考虑几何非线性的影响,参考一般非线性有限元理论可得:
上式中:为线性刚度矩阵;
为非线性刚度矩阵;
为节点不平衡力;
风雪载荷都转换为单元等效节点载荷。由于膜和索只能受拉,不能受压。这样如果在计算中,膜内出现压应力,则会产生褶皱;如果索内产生压应力,便会松弛。我们可以根据膜单元内的主应力来判断是否会出现褶皱,而根据索内的轴向力来判断是否会出现松弛。
用ANSYS进行分析时,会由于膜结构的高度非线性特征带来极不容易收敛的问题,下面对膜结构整体模型分析加强收敛提几条建议:
1)求解方法。本质上说,只要结构本身是稳定体系,无论是变刚度迭代求解,或是常刚度迭代法,其结果均是唯一的,差别通常只是体现在数值求解误差上;
2)载荷步划分的问题。由于唯一提升是一步完成的,所以,划分合理的载荷子步数将缓解非线性程度。过多的子步数会造成数值累计误差增大,求解效率降低,过少的子步数对非线性收敛不利。通常将载荷划分为15~30个子步数,求解精度和求解效率都可以得到很好的保证。
3)收敛准则问题。非线性计算常用的收敛准则有位移收敛准则和力收敛准则。其中位移收敛准则要求第i此迭代产生的位移增量和总位移精确值
之比在一定精度内,即:
式中表示矢量的二范数,作为精度判断的基数,即要求:
相应的力收敛准则为:
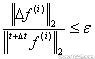
在张力结构计算中,通常采用力收敛准则就可以保证结果的收敛精度,当然也可以采用位移收敛准则,或者混合收敛准则。力收敛准则的控制精度在2%~5%之间即可。支座提升法,倘若收敛困难,控制精度可以取到5%。当力收敛准则失效时,往往是由于求解过程中数值稳定性问题,而非结构稳定性造成的,这个时候换用位移收敛准则是个不错的选择。由于位移收敛准则存在假收敛问题,因此对求解结果的判定非常重要。这个问题有两种比较有效的解决方法:将位移收敛初始容差设定在1%以下,在保证收敛的条件下,将收敛容差逐步降低,经过多次运算,直到相邻误差趋于平稳即可;优先采用二范数收敛准则,必要时可采用无穷数收敛准则。
下面进行膜结构的载荷加载。初始模型见文章“用ANSYS解决膜结构的初始形态问题”。经过多次自平衡迭代,找到最小平衡曲面后,进行膜面加载。膜表面受风压大小为500Pa,下面将压力转换为等效节点力。膜面节点力计算公式为 , 为膜面压力, 为膜面空间体积, 为膜面节点总数,经过相应计算,膜面各节点所受力 ,图1是加载后的模型(同时施加了膜和索的重力)。
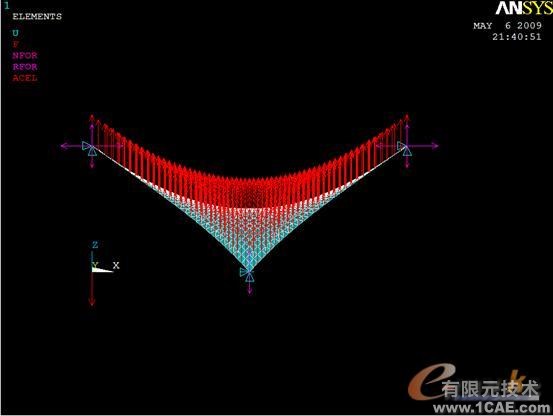
图1
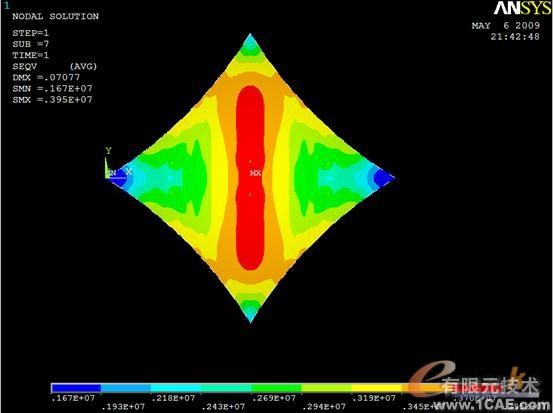
图2
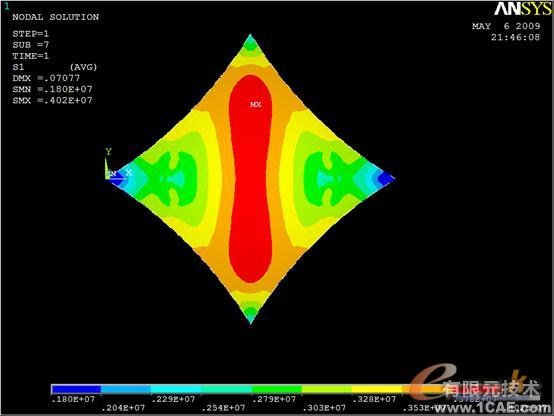
图3
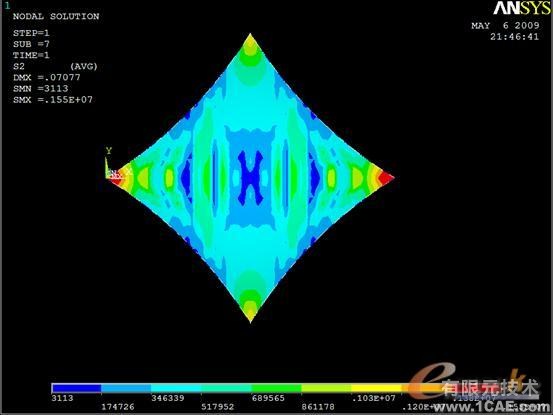
图4
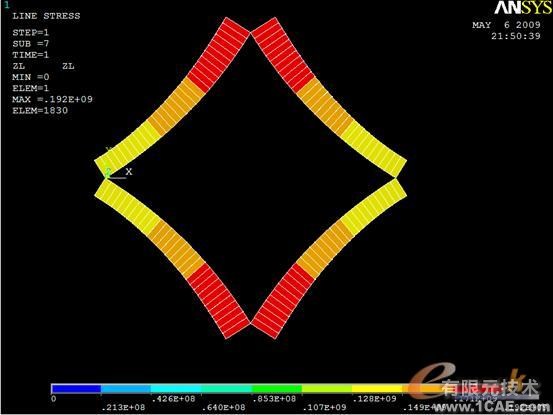
图5
图2显示的是膜中Von Mises应力分布图。从图中可以看出,膜结构在此风载作用下,中心位移最大,为0.07077m。图3和图4分别显示的是第一主应力和第二主应力,通过观察第一和第二主应力,就可以确定膜面是否发生褶皱,膜面最小第二主应力为3113Pa,大于0。因此,可以认为在此风载作用下,膜面不会发生褶皱。图5显示的是索中的轴向应力,可以看出轴向最小拉应力为1.28e8,远大于0,可以作出结论:索处于受拉状态,所以不会出现松弛现象。
相关标签搜索:膜结构的载荷分析 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训 Abaqus培训 Autoform培训 有限元培训 Solidworks培训 UG模具培训 PROE培训 运动仿真






